② 没有可恶的后台工作人员随时随刻调动你们的深渊爆率和出货的东西,例:魔战四件了?冰雪精炼齐了?真男人手搓光和安图左都有了?呵呵,我就是不给你魔战肩.继续砸钱吧!
- 其实真实计算大概是这样的:(大概)60%出大牛40%出小牛,大牛出九件货小牛出六件货,每件货是ss的概率为p.大牛一盘爆金光的概率(含N黄)为1-(1-p)^9小牛为1-(1-p)^6, 综合一盘见光概率为1-0.6(1-p)^9-0.4(1-p)^6≈7.8p. 但这p值出了腾讯的那群坏蛋蛋蛋蛋们没人知道…所以为了实用我们还是用4%吧。
③ 刷的图是格蓝迪. 爆出的为80~85ss. 80以上ss装备词典有362件,其中含"荒古"的有28件,"贪食"的有11件,"源助力"的有5件.362-28-11-5=318件可以刷出来的ss.(万恶之源,出现无穷次.我现在做计算看到这个数字都想吐)
⑤ 不卖装备无色不分解ss不狗眼换票…这样那样的算起来太累…(狗眼爆率多少?留不留非目标可以用的ss? 出第二个三个同样的要不要分解?分解后换的票又出了多少?啊啊啊啊啊啊!)
【重点解释】
本文重要概念:
① 刷出xxxxxx需要的xxxxxx的期待值:期待值就是…假设有一堆人都在刷xxxxxx,每个人都刷到毕业,平均下来用了xxxxxx票就成为了我们的期盼值.但在游戏里我们在毕业的人群中统计这个值会比算出来的低.这是为什么呢?其实很简单…后面会揭示,脸黑的人根本就刷不到毕业…毕业的都是一些脸相对比较白的自然就把数值拉低了…
② 有xx%的人在刷了xxxxxx票后刷出了xxxxxx:这是根据概率估算上面那群人,有百分之多少的人在刷了xxxxxx票之前毕业。
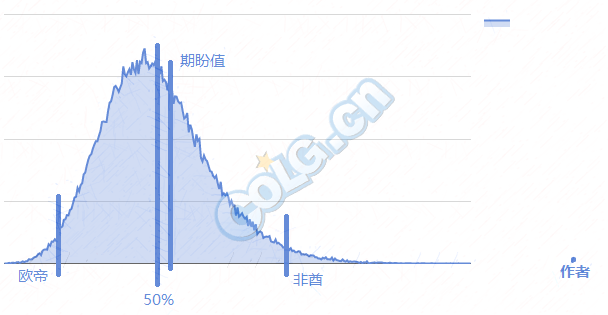
-并不是50%的人就会在期待值毕业.由于脸白的人再少刷的票也不会是负数(…出的狗眼ss换的票超过买的票? 把那个欧洲细作拖出去枪毙个十分钟)脸黑的却可以多正常人几倍,期待值被往高拉了一些.但越是需要的票多这两个数值越接近。
用几何学的看法来,50%就是左右面积一样的地方,而期盼值就是图形的重心那一条线
③ “我怎么没刷xxxxxx票,就毕业了xx xx和xx?”
- 有可能是因为你脸太白,但更多的是因为有很多种毕业的搭配.举例假设如果只有10%的人在10W票中毕业了魔战,85可有10套ss防具套装呢.这10W票中你十套没一套毕业的概率只有(1-10%)^10≈35%,也就是说你毕业了至少一件防具的概率有65%.这还是没算80ss防具,还有更容易毕业的首饰系列的结论。
- 更极端的例子:你洗一副54张的扑克牌洗了N遍后,随机弄出你这样一副扑克牌的概率是54!-1=2.31x10^71分之一.换句话说,即使地球上一直有70亿人,每个人一秒洗一次牌,然后宇宙中有一亿亿亿亿这样的地球的话,洗一亿亿年洗出你这一副牌的概率也还不到千分之一.但你偏偏就洗出来了…何解?
由于二项式分布的不规则性,这两个可能有一定量的偏差.具体后文自己看吧…
【系数说明】
好吧我们开始吧 (我废话真多…)。
有318种能爆的ss,结果就是平均每318件ss爆特定一件.虽然这看上去简单,其实具体得出这结论还挺复杂的…
- 第一件爆想要的出来的概率为1/318
- 第二件才爆出来,概率为(317/318)(第一件没爆出来) x (1/318)
- 第三件,第四件,第N件…,概率为 (317/318)^3, 4, N… x (1/318)
- 然后我们的期盼值就是E=1x(1/318)+2x(317/318)(1/318)+3x(317/318)2(1/318)…
- 为了消除一些苦恼销项: (317/318)E= 1x(317/318)(1/318)+2x(317/318)2(1/318)…
- 一式减二式: (1/318)E=(1/318)(1+317/318+(317/318)2+(317/318)3+…)
- 再减去一次(317/318)E, 我们得出(1/318)E=1→E=318
- 铛铛铛铛!
这就表明,刷单一一件ss的期待值是318件ss,根据我们4%的深渊爆率,刷一件ss的票数期待值为318/0.04*24=190800票.也就是平均刷出你想要的ss(魔战胸何在!)需要刷接近20W票.这是38E金币, 7632元,和159天每天一小时的不懈劳作。
但如果要计算有50%的概率出目标ss需要的票数,计算方法有点不一样.首先,我们需要算出每一次深渊爆出你想要的ss的概率,因为两个统计分布互相单独算的话并不能还原原来的整体分布。
- 4%(深渊爆货率)*(1/318)(是想要的的概率)=1/7950(一盘深渊出你要的东西的概率)
- 1-1/7950=7949/7950(一盘深渊不出你要的东西的概率… 都是泪)
- 1-50%=50%←剩下的没出要的ss的概率
- (7949/7950)n=50%←N次深渊后还没出要的ss的概率=50%,这里的50%是上面的第二个50%
- n=(log 50%)/(log 7949/7950)=5510.17次深渊=132244票
这数字代表有50%的人在132244票之前刷出了自己要的一件目标ss,也有50%的人要刷超过这数值。
【出货花销】
有人欢喜有人愁… 但总体情况还是挺让人担忧的… 2011年6月出的70版本, 2013年6月出的85, 什么时候100版本会来把我们辛苦刷的ss全部变成废品呢~
这是单件, 有些人就要发问了: 如果我有两三种武器可以毕业呢? 如果我不转职练到86刷起深渊出什么转什么(佩服大神!), 这样能多快刷出要的呢? 好的, 我再来算, 拿五件作为例子吧:
对于期盼值, 爆ss刷出318中5件任意一件为318/5 (得出来的方法和之前一样)
318/5/0.04*24=38160票=7.6E金币=1526.4元
每盘不爆货的概率降低到了1589/1590, 于是我们获得到了新的一批数据
欧帝(1%): 383.4票, 767W金币, 15.33块钱, 0.3天 (囧)
雪白(10%): 4019.3票, 8039W金币, 160.77元, 3.35天
白嫩(20%): 8512票, 1.7E金币, 340.5元, 7.09天
亚裔(50%): 26442, 5.29E, 1050, 22
古铜(80%): 61397, 12.3E, 2460, 51
黝黑(90%): 87839, 17.6E, 3500, 73
非酋(99%): 175678, 35.1E, 7000, 146
那无尽的夜空(99.99%): 351356, 70.3E, 14000, 293
【举个栗子】
到现在, 有些在攒套装的人不耐烦了: 我魔战要刷多久才能毕业啊? 一套幽魂得花多少才能刷出来? 不会是上面的数据乘以五吧! 其实, 同时刷几件的情况比较特殊, 因为最开始的一件虽然爆率是类似我们讨论的第二种情况的, 但越刷越容易重复. 最后一件就成了我们之前讨论的第一种情况了… 现在, 我来算下从0起步, 刷一套防具的期望值吧. 一缺四三缺二神马之类的自己衍生吧~ 搭配几件也是同样的道理哦~ (比说肩戒矛就是缺三件的情况)
期盼值=(318/5+318/4+318/3+318/2+318)/0.04*24=435660票, 87.1E, 17426.4元, 363天
由于情况复杂了(每件), 概率变得极其难算. 现在这个几个二项式合并起来我即使请教了统计专业的学长也没得到立刻的答案. 但由于数字变得很大, 二项式分布已经接近于标准分布了(某学长大人还在拼命喊“不够大!”无视。). 所以我们可以假设二项式的分布的中心与标准分布吻合, 从每件装备最原始的爆率出发来估算所需要的票数:
假设刷了那么多次后, 每一件要刷的出的概率都是p. 出齐的概率是p^5=50%, p就成为了2-1/5=87.06%. 设N次深渊使原来爆率只有1/7950的物品拥有87.06%的爆率, 我们得到需要 (7949/7950)n=13.94%→n=16252.5次深渊. 24n=390059票(距离435660还是差了好多… 啊啊啊啊啊不管了!), 也就是78E, 15602元, 和325天。
数据再次奉上:
欧帝: 96858票, 19.4E, 3874元, 81天
雪白: 190186, 38.0E, 7600, 158
白嫩: 246152, 49.2E, 9846, 205
亚裔: 390000, 78E, 15600, 325
古铜: 597000, 119E, 23900, 498
黝黑: 738000, 148E, 29500, 615
非酋: 1180000, 237E, 47400, 987
那无尽的夜空: 2060000, 413E, 82600, 1720
对,你没看错,我也没算错(…应该吧…)虽然会有出入,但在数量级上是不会错的.要刷出一套ss防具,除了幸运的10%之外,其他人都要刷超过20W票.如果你碰巧属于脸黑的那20%,请先准备好60W票再来考验现实的残酷吧…
说到这里,有很重要的一点要提醒大家:我的所有的计算都是基于最开始奠定的两点的:所有ss爆率相同,以及没有人在后台捣鬼.如果我的计算没有人验证出问题,就得好好地去验证这两点的成立与否啦。
【结论总结】
最后总结,还是那个万年不变的真理.深渊顾名思义就是一个很大的坑,能从中间一套ss走出来的, 不是脸帝就是托.肝在残酷的现实里不顶一分钱。
嘛,就这样吧~虽然知道爆率那么残酷…
我为什么还是那么想刷深渊呢?
【图示说明】